Binary Search Trees
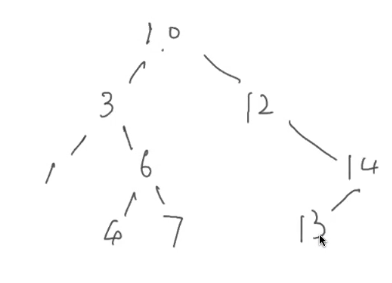
Here is a link to a good visualizer
SearchBST
Every time we move a level, we cut the problem in half
TreeNode *searchBST(TreeNode* root, int target){
if(root == NULL ){
return NULL;
}
if(target == root.val){
return root;
}
if(target<root.val){
searchBST(root->left,target);
}
if(target>root.val){
searchBST(root->right,target);
}
}
Insert An Element
typically, in a binary search tree, the value must be unique
TreeNode* insertBST(TreeNode* root, int val){
if(root == NULL){
return newTreeNode(val);
}
if(val<root.val){
root->left = insertBST(root->left,val);
}
if(val > root.val){
root->right = insertBST(root->right, val);
}
return root;
}
Deleting an Element
Deleting an element requires examining 3 cases
- No Child
- Only 1 Child
- 2 children
No Children
This is the most straight forward, you just remove the node and set the pointer to that node to NULL.
One Child
With one child, you remove the node and set the child to the position of the removed node
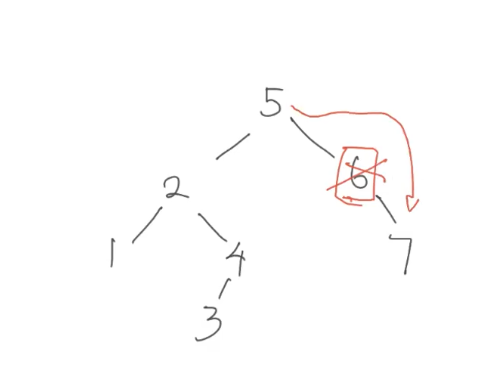
you must create a temporary pointer
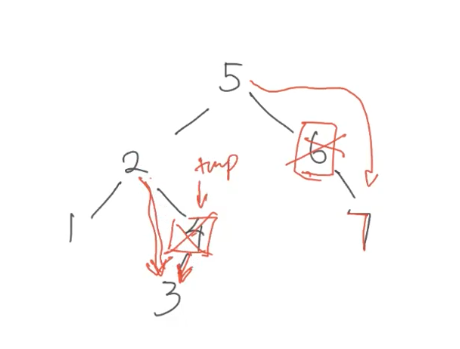
Two Children
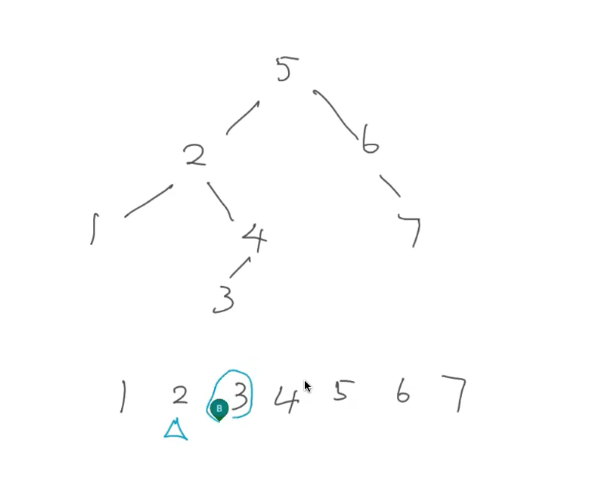
With two children, you need to find the In-Order successor or predecessor.
If we want to remove 2:
If the node we're replacing the deleted node with ALSO has a child. In the case of one child, the child takes the place of the position of the successor.
To find in-order predecessor: Move one space left, then as far right as possible.
To find in-order successor: move one space right, then as far left as possible.