CSS 430 Book Notes Chapter 6 - Synchronization Tools
Background
A cooperating process is one that can affect or be affected by other processes executing in the system. Cooperating processes can either directly share a logical address space (that is, both code and data) or be allowed to share data only through shared memory or message passing.
Notice that we have arrived at the incorrect state "count == 4", indicating that four buffers are full, when, in fact, five buffers are full. If we reversed the order of the statements at �4 and �5, we would arrive at the incorrect state "count == 6".
We would arrive at this incorrect state because we allowed both processes to manipulate the variable count concurrently. A situation like this, where several processes access and manipulate the same data concurrently and the outcome of the execution depends on the particular order in which the access takes place, is called a race condition.
To guard against the race condition above, we need to ensure that only one process at a time can be manipulating the variable count. To make such a guarantee, we require that the processes be synchronized in some way.
6.2 The critical-section problem
Consider a system consisting of n processes {p0, p1, …, P(n−1)}. Each process has a segment of code, called a critical section, in which the process may be accessing — and updating — data that is shared with at least one other process.
when one process is executing in its critical section, no other process is allowed to execute in its critical section.
The critical-section problem is to design a protocol that the processes can use to synchronize their activity so as to cooperatively share data.
-Each process must request permission to enter its critical section
The section implementing this request is the entry section
The critical section may be followed by an exit section
General structure of a typical process

A solution to the critical section problem must satisfy these three requirements:
- Mutual exclusion.: If process P(i) is executing in its critical section, then no other processes can be executing in their critical sections.
- Progress:: If no process is executing in its critical section and some processes wish to enter their critical sections, then only those processes that are not executing in their remainder sections can participate in deciding which will enter its critical section next, and this selection cannot be postponed indefinitely.
- Bounded Waiting: There exists a bound, or limit, on the number of times that other processes are allowed to enter their critical sections after a process has made a request to enter its critical section and before that request is granted.
We can make no assumption concerning the relative speed of the a processes.
Two general approaches are used to handle critical sections in operating systems: preemptive kernels and nonpreemptive kernels.
- Preemptive Kernel: allows a process to be preempted while it is running in kernel mode.
- Nonpreemptive kernel: A nonpreemptive kernel does not allow a process running in kernel mode to be preempted; a kernel-mode process will run until it exits kernel mode, blocks, or voluntarily yields control of the CPU.
A nonpreemptive kernel is essentially free from race conditions on kernel data structures, as only one process is active in the kernel at a time.
6.3 Peterson's Solution
Peterson's solution is a software based solution to the critical section problem.
- Does not necessarily work correctly on all architectures
Peterson's solution is restricted to two process that switch back and forth in their critical sections.
The processes are
Petersons's solution requires the processes share two data items:
int turn;
bool flag[2];
turn indicates whose turn it is to enter the critical section. If turn == i then flag is used to indicate whether or not a process is ready to enter a critical section.
For example, if flag[i] == true;
while (true) {
flag[i] = true;
turn = j;
while (flag[j] && turn == j)
;
/* critical section */
flag[i] = false;
/*remainder section */
}
To enter the CS, flag[i] to true and then sets turn to value j. This asserts that if the other process wishes to enter the critical section, it can do so.
If both processes try to enter at the same time, turn will be set to both i and j at the same time. Only one of these arguments will last as the other will be overwritten immediately.
The value of turn determines which determines which of the two processes is allowed to enter its critical section first.
To prove this is correct, you need to show:
- Mutual exclusion is preserved.
- The progress requirement is satisfied.
- The bounded-waiting requirement is met
6.4 Hardware support for synchronization
Peterson's Solution is a software solution, however software solutions are not guaranteed to work on modern architectures.
Below are three hardware instructions that help solve the critical section problem
Memory Barriers
How a computer architecture determines what memory guarantees it will provide to an application program is known as its memory model. In general, a memory model falls into one of two categories:
-
Strongly ordered, where a memory modification on one processor is immediately visible to all other processors.
-
Weakly ordered, where modifications to memory on one processor may not be immediately visible to other processors.
computer architectures provide instructions that can force any changes in memory to be propagated to all other processors, thereby ensuring that memory modifications are visible to threads running on other processors. These are known as memory barriers or memory fences
If we add a memory barrier operation to Thread 1
while (!flag)
memory_barrier();
print x;
We guarantee the value of flag is loaded before x
x = 100;
memory_barrier();
flag = true;
Hardware Instructions
Many modern computer systems provide special hardware instructions that allow us either to test and modify the content of a word or to swap the contents of two words atomically—that is, as one uninterruptible unit.
Rather than discussing one specific instruction for one specific machine, we abstract the main concepts behind these types of instructions by describing the test_and_set() and compare_and_swap() instructions.
Thus, if two test_and_set() instructions are executed simultaneously (each on a different core), they will be executed sequentially in some arbitrary order. If the machine supports the test_and_set() instruction, then we can implement mutual exclusion by declaring a boolean variable lock, initialized to false.
Test and Set Definition
boolean test_and_set(boolean *target) {
boolean rv = *target;
*target = true;
return rv;
}
Mutual-exclusion implementation with test and set
do {
while (test_and_set(&lock))
; /* do nothing */
/* critical section */
lock = false;
/* remainder section */
} while (true);
The compare_and_swap() instruction uses a different mechanism that is based on swapping the content of two words.
The CAS instruction operates on three operands. The operand value is set to new_value only if the expression (*value == expected) is true. Regardless, CAS always returns the original value of the variable value.
Compare and Swap Instruction Definition
int compare_and_swap(int *value, int expected, int new_value) {
int temp = *value;
if (*value == expected)
*value = new_value;
return temp;
}
A global variable (lock) is declared and is initialized to 0. The first process that invokes compare_and_swap() will set lock to 1. It will then enter its critical section, because the original value of lock was equal to the expected value of 0. Subsequent calls to compare_and_swap() will not succeed, because lock now is not equal to the expected value of 0. When a process exits its critical section, it sets lock back to 0, which allows another process to enter its critical section.
Mutual exclusion with compare and swap
while (true) {
while (compare_and_swap(&lock, 0, 1) != 0)
; /* do nothing */
/* critical section */
lock = 0;
/* remainder section */
}
The above does not satisfy the bounded waiting requirement
To do so, we modify it slightly by adding
boolean waiting[n];
int lock;
The elements in the waiting array are initialized to false, and lock is initialized to 0. To prove that the mutual-exclusion requirement is met, we note that process �� can enter its critical section only if either waiting[i] == false or key == 0. The value of key can become 0 only if the compare_and_swap() is executed. The first process to execute the compare_and_swap() will find key == 0; all others must wait. The variable waiting[i] can become false only if another process leaves its critical section; only one waiting[i] is set to false, maintaining the mutual-exclusion requirement.
Mutual Exclusion bounded waiting compare and swap
while (true) {
waiting[i] = true;
key = 1;
while (waiting[i] && key == 1)
key = compare_and_swap(&lock,0,1);
waiting[i] = false;
/* critical section */
j = (i + 1) % n;
while ((j != i) && !waiting[j])
j = (j + 1) % n;
if (j == i)
lock = 0;
else
waiting[j] = false;
/* remainder section */
}
Atomic Variables
Provides atomic operations on basic data types such as integers and booleans.
Most systems that support atomic variables provide special atomic data types as well as functions for accessing and manipulating atomic variables. These functions are often implemented using compare_and_swap() operations. As an example, the following increments the atomic integer sequence:
increment(&sequence);
void increment(atomic_int *v)
{
int temp;
do {
temp = *v;
}
while (temp != compare_and_swap(v, temp, temp+1));
}
6.5 Mutex Locks
Operating-system designers build higher-level software tools to solve the critical-section problem. The simplest of these tools is the mutex lock.
Mutex is short for mutual exclusion
a process must acquire the lock before entering a critical section; it releases the lock when it exits the critical section. The acquire() function acquires the lock, and the release() function releases the lock
while (true) {
acquire lock
critical section
release lock
remainder section
}
A mutex lock has a boolean variable available whose value indicates if the lock is available or not. If the lock is available, a call to acquire() succeeds, and the lock is then considered unavailable. A process that attempts to acquire an unavailable lock is blocked until the lock is released.
Acquire definition
acquire() {
while (!available)
; /* busy wait */
available = false;
}
Release Definition
release() {
available = true;
}
Locks are either contended or uncontended. A lock is considered contended if a thread blocks while trying to acquire the lock. If a lock is available when a thread attempts to acquire it, the lock is considered uncontended. Contended locks can experience either high contention (a relatively large number of threads attempting to acquire the lock) or low contention (a relatively small number of threads attempting to acquire the lock.) Unsurprisingly, highly contended locks tend to decrease overall performance of concurrent applications.
The main disadvantage of the implementation given here is that it requires busy waiting. While a process is in its critical section, any other process that tries to enter its critical section must loop continuously in the call to acquire().
The type of mutex lock we have been describing is also called a spinlock because the process "spins" while waiting for the lock to become available.
Spinlocks do have an advantage, however, in that no context switch is required when a process must wait on a lock,
6.6 Semaphores
A semaphore S is an integer variable that, apart from initialization, is accessed only through two standard atomic operations: wait() and signal()
Wait Definition
wait(S) {
while (S <= 0)
; /* busy wait */
S--;
}
Signal Definition
signal(S) {
S++;
}
All modifications to the integer value of the semaphore in the wait() and signal() operations must be executed atomically.
In addition, in the case of wait(S), the testing of the integer value of S (S ≤ 0), as well as its possible modification (S--), must be executed without interruption.
The value of a counting semaphore can range over an unrestricted domain. The value of a binary semaphore can range only between 0 and 1.
In fact, on systems that do not provide mutex locks, binary semaphores can be used instead for providing mutual exclusion.
Counting semaphores can be used to control access to a given resource consisting of a finite number of instances.
The semaphore is initialized to the number of resources available. Each process that wishes to use a resource performs a wait() operation on the semaphore (thereby decrementing the count). When a process releases a resource, it performs a signal() operation (incrementing the count). When the count for the semaphore goes to 0, all resources are being used. After that, processes that wish to use a resource will block until the count becomes greater than 0.
To overcome this problem of busy waiting, we can modify the definition of the wait() and signal() operations as follows:
When a process executes the wait() operation and finds that the semaphore value is not positive, it must wait. However, rather than engaging in busy waiting, the process can suspend itself.
The suspend operation places a process into a waiting queue associated with the semaphore, and the state of the process is switched to the waiting state. Then control is transferred to the CPU scheduler, which selects another process to execute.
A process that is suspended, waiting on a semaphore S, should be restarted when some other process executes a signal() operation. The process is restarted by a wakeup() operation, which changes the process from the waiting state to the ready state.
To implement semaphores under this definition, we define a semaphore as follows:
typedef struct {
int value;
struct process *list;
} semaphore;
Each semaphore has an integer value and a list of processes list. When a process must wait on a semaphore, it is added to the list of processes. A signal() operation removes one process from the list of waiting processes and awakens that process.
Now wait can be defined as
wait(semaphore *S) {
S->value--;
if (S->value < 0) {
add this process to S->list;
sleep();
}
}
and signal can be defined as:
signal(semaphore *S) {
S->value++;
if (S->value <= 0) {
remove a process P from S->list;
wakeup(P);
}
}
The sleep() operation suspends the process that invokes it. The wakeup(P) operation resumes the execution of a suspended process P
If a semaphore value is negative, its magnitude is the number of processes waiting on that semaphore.
The list of waiting processes can be easily implemented by a link field in each process control block (PCB). Each semaphore contains an integer value and a pointer to a list of PCBs. One way to add and remove processes from the list so as to ensure bounded waiting is to use a FIFO queue, where the semaphore contains both head and tail pointers to the queue.
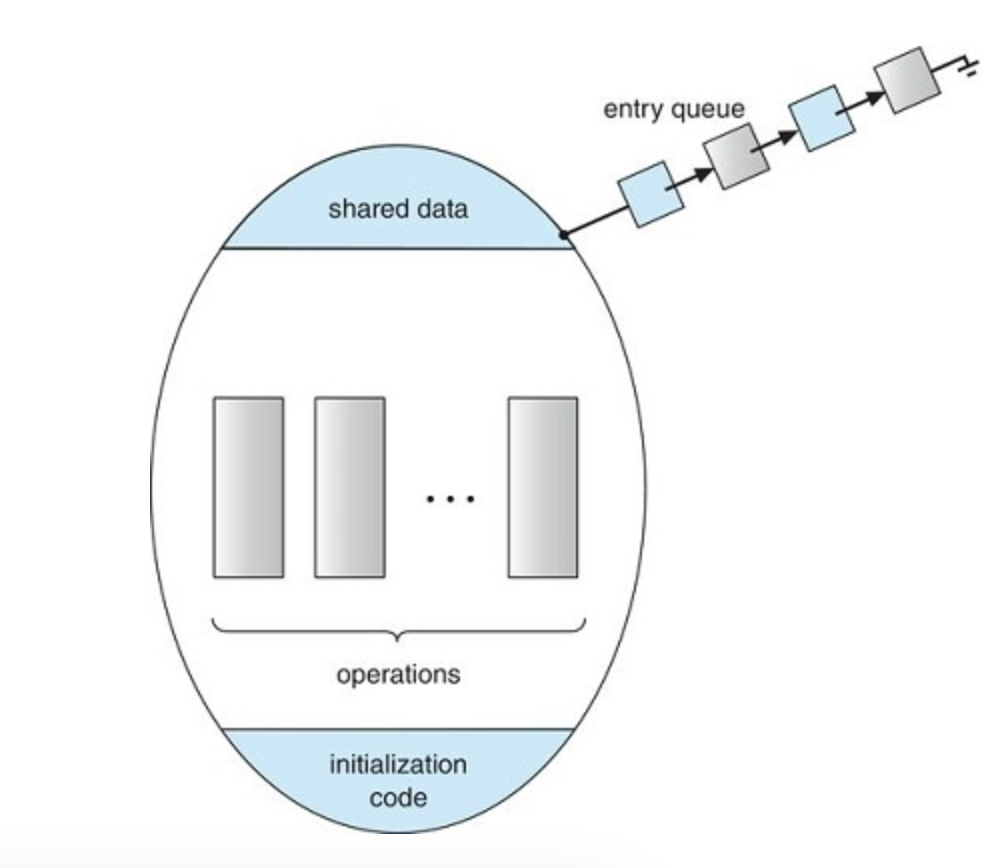
6.7 Monitors
a monitor is a high level synchronization construct
A monitor type is an ADT that includes a set of programmer-defined operations that are provided with mutual exclusion within the monitor.
The monitor type also declares the variables whose values define the state of an instance of that type, along with the bodies of functions that operate on those variables.
The monitor construct ensures that only one process at a time is active within the monitor. Consequently, the programmer does not need to code this synchronization constraint explicitly
We also need to define additional synchronization mechanisms. These mechanisms are provided by the condition construct. A programmer who needs to write a tailor-made synchronization scheme can define one or more variables of type condition:
condition x,y
The only operations that can be invoked on a condition variable are wait() and signal(). The operation x.wait() means that the process invoking this operation is suspended until another process invokes x.signal()
Pseudocode syntax of a monitor
monitor monitor name
{
/* shared variable declarations */
function P1 ( . . . ) {
. . .
}
function P2 ( . . . ) {
. . .
}
.
.
.
function Pn ( . . . ) {
. . .
}
initialization_code ( . . . ) {
. . .
}
}
Schematic view of monitor
Monitor with condition variables
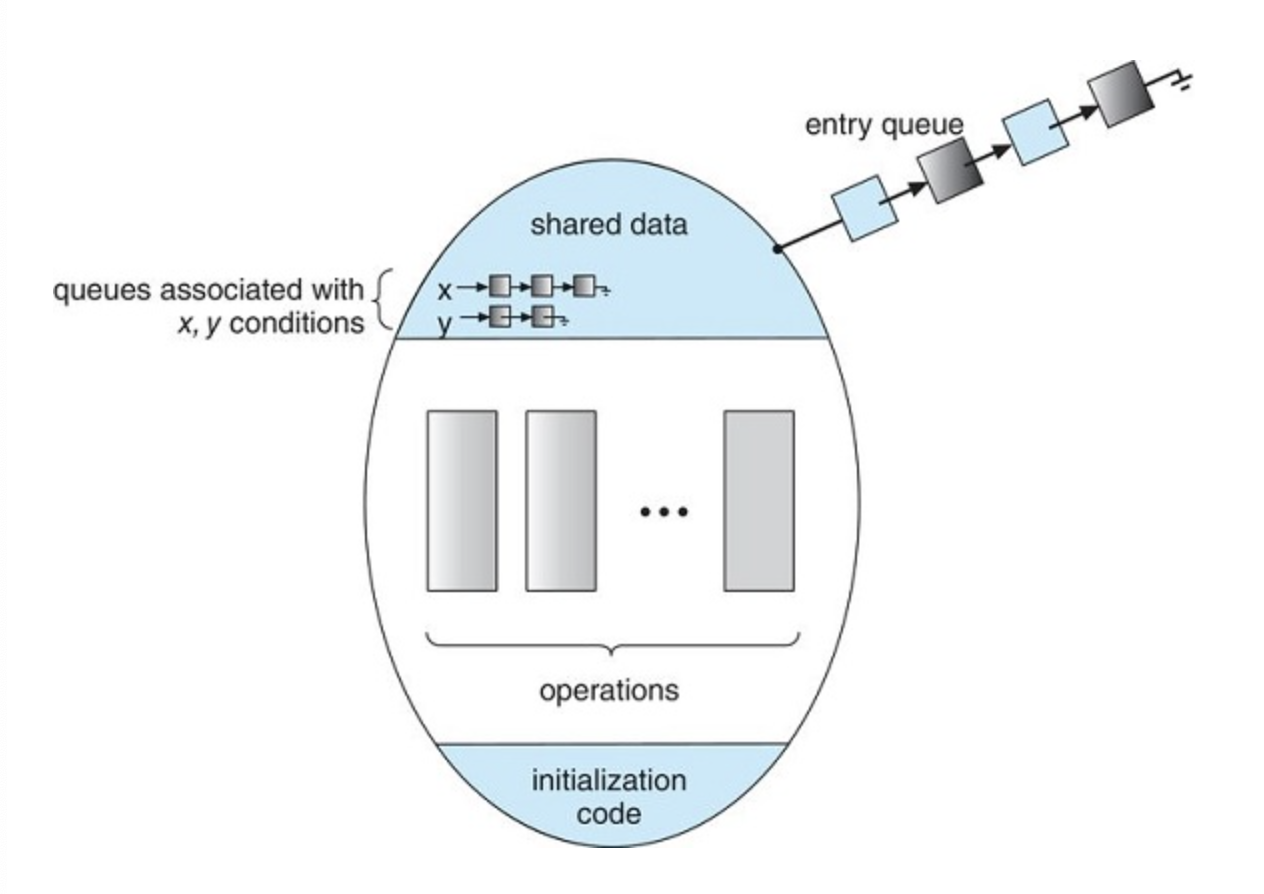
Suppose that, when the x.signal() operation is invoked by a process x. Clearly, if the suspended process
-
Signal and wait. P either waits until Q leaves the monitor or waits for another condition.
-
Signal and continue. Q either waits until P leaves the monitor or waits for another condition.
Monitors With Semaphores
For each monitor, a binary semaphore mutex (initialized to 1) is provided to ensure mutual exclusion. A process must execute wait(mutex) before entering the monitor and must execute signal(mutex) after leaving the monitor.
wait(mutex);
…
body of F
…
if (next_count > 0)
signal(next);
else
signal(mutex);
x.wait()
x_count++;
if (next_count > 0)
signal(next);
else
signal(mutex);
wait(x_sem);
x_count--;
x.signal()
x_count++;
if (next_count > 0)
signal(next);
else
signal(mutex);
wait(x_sem);
x_count--;
Resuming processes within a monitor
If several processes are suspended on condition x, and an x.signal() operation is executed by some process, then how do we determine which of the suspended processes should be resumed next?
The conditional-wait construct can be used. This construct has the form x.wait(c) where wait() operation is executed. The value of x.signal() is executed, the process with the smallest priority number is resumed next.
6.8 Liveness
Liveness refers to a set of properties that a system must satisfy to ensure that processes make progress during their execution life cycle. A process waiting indefinitely under the circumstances just described is an example of a "liveness failure."
Deadlock
The implementation of a semaphore with a waiting queue may result in a situation where two or more processes are waiting indefinitely for an event that can be caused only by one of the waiting processes. The event in question is the execution of a signal() operation. When such a state is reached, these processes are said to be deadlocked.
Priority Inversion
A scheduling challenge arises when a higher-priority process needs to read or modify kernel data that are currently being accessed by a lower-priority process—or a chain of lower-priority processes.
This liveness problem is known as priority inversion, and it can occur only in systems with more than two priorities. Typically, priority inversion is avoided by implementing a priority-inheritance protocol. According to this protocol, all processes that are accessing resources needed by a higher-priority process inherit the higher priority until they are finished with the resources in question.
6.9 Evaluation
he following guidelines identify general rules concerning performance differences between CAS-based synchronization and traditional synchronization (such as mutex locks and semaphores) under varying contention loads:
-
Uncontended. Although both options are generally fast, CAS protection will be somewhat faster than traditional synchronization.
-
Moderate contention. CAS protection will be faster—possibly much faster—than traditional synchronization.
-
High contention. Under very highly contended loads, traditional synchronization will ultimately be faster than CAS-based synchronization.