Data Driven Science & Engineering - Machine Learning, Dynamical Systems, and Control
Part of the Embedded.fm Bookclub
Book Link
Chapter 1 Dimensionality Reduction and Transforms
The SVD provides a stable matrix decomposition that is guaranteed to exist and can me used for many purposes
The SVD can be used to obtain "low-rank" approximations to matrices and perform pseudo inverses of non-square matrices to find a solution to a system of equations
The SVD can also be used as the underlying algo of principal component analysis which allows high-dimensional data to be composed into statistically descriptive factors
The SVD generalizes the concept of the Fast Fourier Transform. While the FFT works in idealized settings, the SVD is a more generic data-driven technique. The SVD may be thought of as providing a basis that is tailored to specific data, as opposed to the FFT which provides a generic basis
In many domains, systems generate data that is a natural fit for large matrices or arrays. EG: a time series of data from an experiment could be arranged into a matrix with each column containing all of the measurements from time
The Data generated by these systems are low rank which means there are jus a few dominant patterns that explain high-dimensional data. The SVD is an efficient method of extracting these patterns
Overview
The SVD Provides a systematic way to determine a low-dimensional approximation to high-dimensional data in terms of dominant patterns.
The SVD is GUARANTEED to exist for any matrix
The SVD an help compute a pseudo-inverse of a non-square matrix which can give us solutions to under or overdetermined matrix equations
The SVD can also be used to de-noise datasets.
The SVD can also characterize the input and output geometry of a linear map between vector spaces.
SVD Definition
Generally we're interested in analyzing a large data set
The columns
The index
In many cases, the state dimension is large (ie millions or billions of DOF). The columns can be thought of as "snapshots" and
The SVD is a unique matrix decomp that exists for every complex valued matrix
The condition that
When
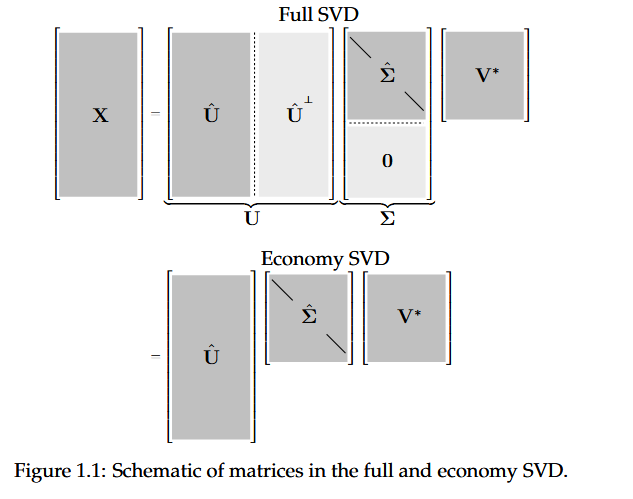
The columns of
Diagonal elements of
Computing the SVD
import numpy as np
X= np.random.rand(5,3) #Create a random data matrix
U,S,V = np.linalg.svd(X,full_matrices=True) #Full SVD
Uhat, Shat,Vhat = np.linalg.svd(X, full_matrices=False) #Economy SVD
1.2 Matrix Approximation
Glossary
| Term | Definition |
|---|---|
| SVD | Singular Value Decomposition |
| PCA | Principal Component Analysis |