Op-Amp

Op-Amps

Operational Amplifiers
Can be configured to do different operations such as: amplification, subtraction, addition, differentiation, integration.

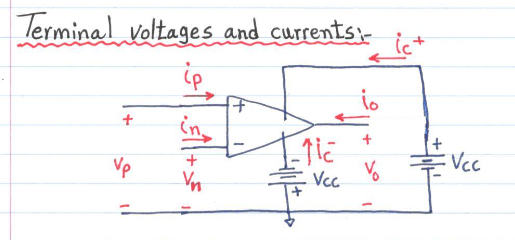
Screen Shot 2021-02-23 at 3.11.21 PM.png

Voltages are considered voltage rises.
All current flows into the Op-Amp.

The output voltage $V_{o}$ is a function of the difference between the input voltages $V_{p} - V_{n}$

Op amps have very high input impedance, but low output impedance

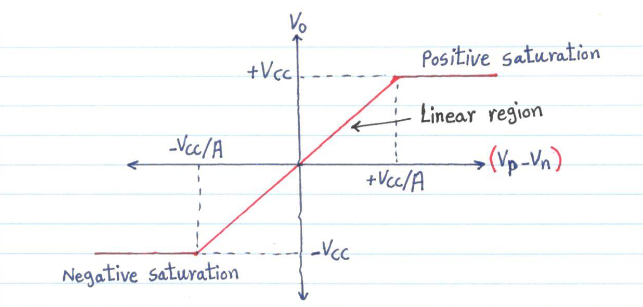
There are different regions of operation of an Op-Amp:

Negative Saturation: This occurs when $V_{o}$ is less than $- V_{c c}$
Linear Region: This occurs when $V_{o}$ is in between $- V_{c c}$ and $+ V_{c c}$
Positive saturation: When $V_{o}$ is greater than $+ V_{c c}$

There are some assumptions we make with Op-Amps:

1. Voltage Constraint: We assume that $V_{p} = V_{n}$

2. Current Constraint: We assume that $I_{p} = I_{n} = 0$

Gain

Inverting Op Amp

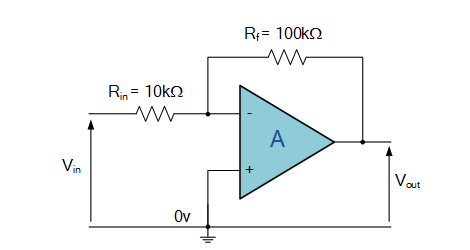
Screen Shot 2021-02-23 at 1.44.18 PM.png
For inverting Op-Amp, Gain = A

$A = \frac{- R_{f}}{R_{1}}$

$V_{o} = \frac{- R_{f}}{R_{1}} \cdot V_{s}$

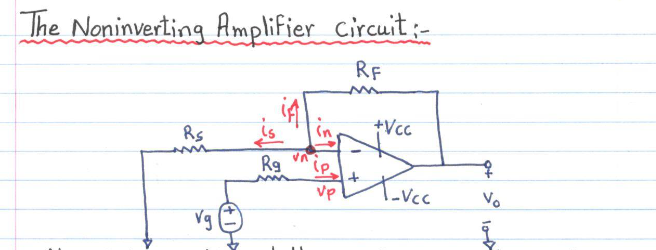
Non-Inverting Op Amp

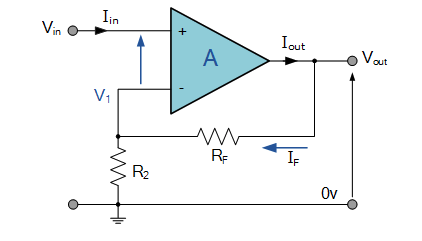
Screen Shot 2021-02-23 at 1.39.13 PM.png

For a non inverting Op Amp your gain = A

$A = \frac{R_{f}}{R_{s}} + 1$

$V_{o} = \frac{R_{f} + R_{s}}{R_{s}} \cdot V_{g}$

Screen Shot 2021-02-23 at 3.24.51 PM.png

Buffer Op-Amp or Voltage Follower Op-Amp

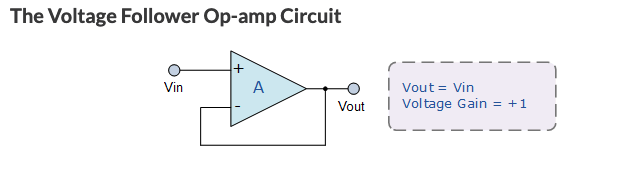
Screen Shot 2021-02-23 at 2.00.10 PM.png
The voltage follower Op-Amp does not amplify the signal. The Gain of voltage follower op-amp is always 1.

Summing Op-Amp

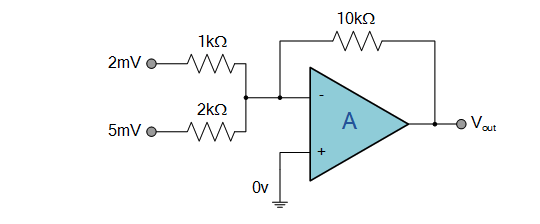
Screen Shot 2021-02-23 at 1.48.32 PM.png
In this case, we still use the equation $A = \frac{- R_{f}}{R_{1}}$ for our gain, however, we need to do it for each branch. SO, for the example above:

$A_{1} = \frac{- 10 k Ω}{1 k Ω}$ and

$A_{2} = \frac{- 10 k Ω}{2 k Ω}$

We can then use the equation $V_{o} = (A_{1} \cdot V_{1}) + (A_{2} \cdot V_{2})$

Therefore using the example above, $V_{o} = (- 10 \cdot 2 m V) + (- 5 \cdot 5 m V) = - 45 m V$

Difference Amplifier

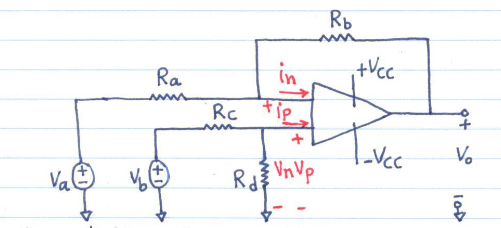
Screen Shot 2021-02-23 at 3.29.22 PM.png
Use Voltage Divider to find $V_{p}$
$V_{p} = \frac{R_{d}}{R_{c} + R_{d}} V_{b}$

Write Kirchoff's Voltage Law equation at the inverting input terminal.

$I_{a} + I_{b} + I_{c} = 0$ , $I_{n} = I_{p} = 0$

$V_{o} = (\frac{R_{b}}{R_{a}} + \frac{R_{b}}{R_{b}}) V_{n} - \frac{V_{a}}{R_{a}} R_{b} \to V_{o} = \frac{R_{b}}{R_{a}} (V_{b} - V_{a})$

Keep in mind that $\frac{R_{a}}{R_{b}} = \frac{R_{c}}{R_{d}}$

To Calculate a voltage source that will not saturate the op-amp use:

$V_{s} = \frac{- R_{1}}{R_{f}} \cdot + V_{c c}$ and $V_{s} = \frac{- R_{1}}{R_{f}} \cdot - V_{c c}$ your answer will be in the form $L o w e r V a l u e \leq V_{s} \leq U p p e r V a l u e$

Op-Amps

1. Voltage Constraint: We assume that Vp=Vn

2. Current Constraint: We assume that Ip=In=0

Gain

Inverting Op Amp

A=−RfR1

Vo=−RfR1⋅Vs

Non-Inverting Op Amp

A=RfRs+1

Vo=Rf+RsRs⋅Vg

Buffer Op-Amp or Voltage Follower Op-Amp

Summing Op-Amp

A1=−10kΩ1kΩ and

A2=−10kΩ2kΩ

We can then use the equation Vo=(A1⋅V1)+(A2⋅V2)

Therefore using the example above, Vo=(−10⋅2mV)+(−5⋅5mV)=−45mV