RC and RL Circuits

RC and RL Circuits are circuits that contain Inductance or Capacitance

RC Circuits

$i_c(t)=C\frac{dv}{dt}$

To think about it abstractly... at t=0, the most current has been placed on a circuit, but no charge has reached a capacitor

"After a long time" means when the capacitor is fully charged.

Once a capacitor is fully charged, there is no current flowing through a circuit, therefore you can replace it with an open circuit

RC Circuit Analysis Video

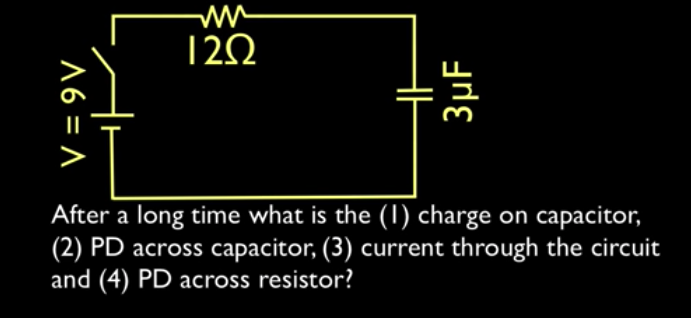
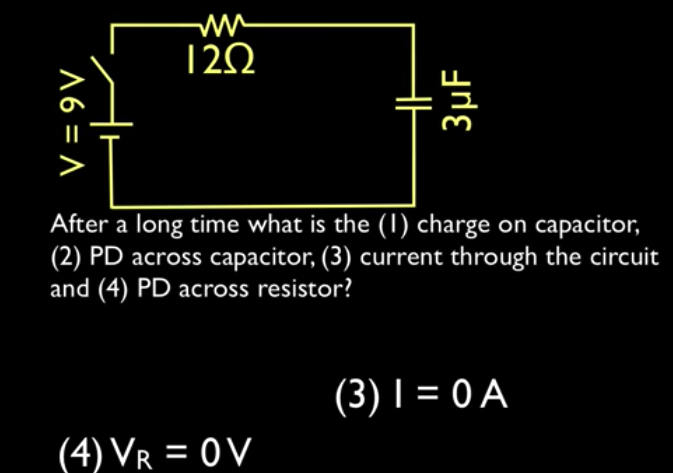
at time = infinity, the voltage of the capacitor = the charge of the battery. The charge of the capacitor is equal to $Q=C\cdot V$

$V(t)=V_b(1-e^{\frac{-t}{RC}})$

$I(t)=I_0(E^{\frac{-t}{RC}})$

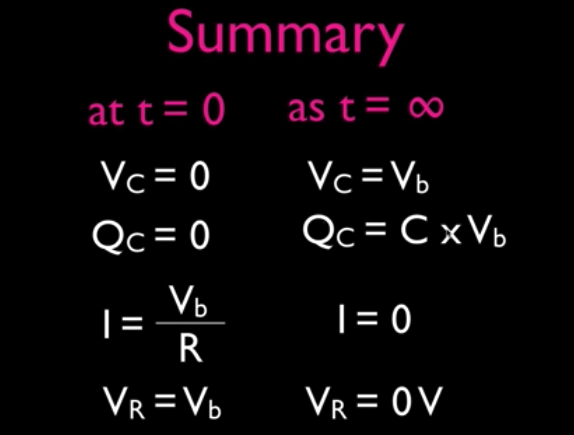
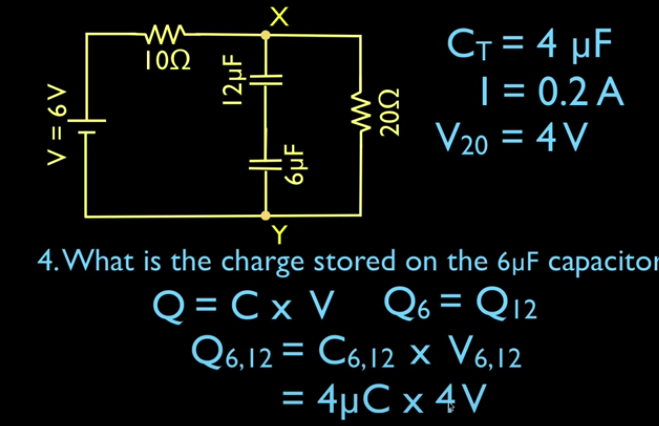
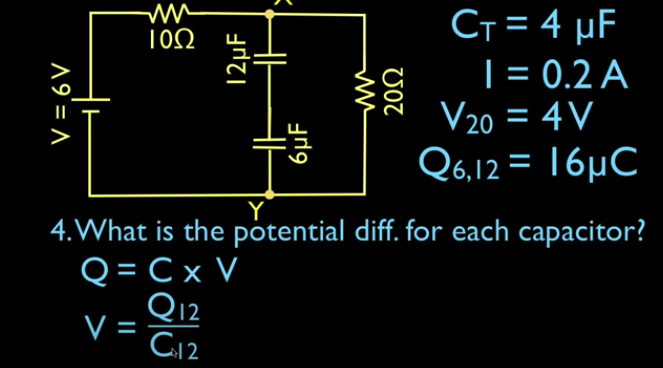
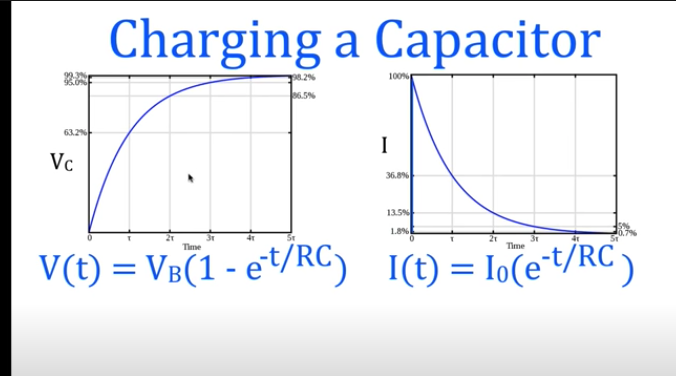
The time constant is designated by $\tau$ and is calculated with the equation $\tau =RC$

RL

Inductors resist changes in current

At t=0 current is zero and V_L = V_S.

"After a long time" an inductor will act as a short circuit.

$V_L=L\frac{di}{dt}$

$V_s=IR+L\frac{di}{dt}$ at t=0

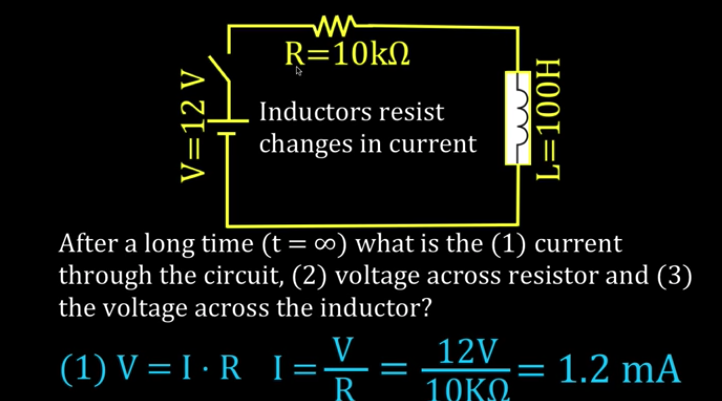
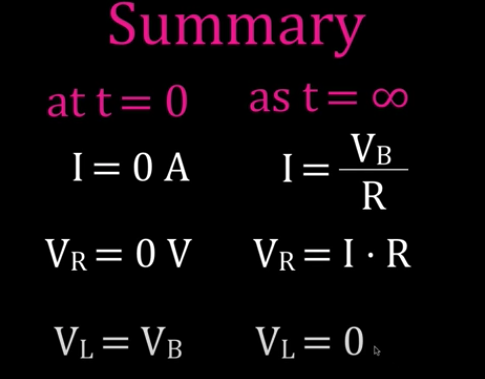
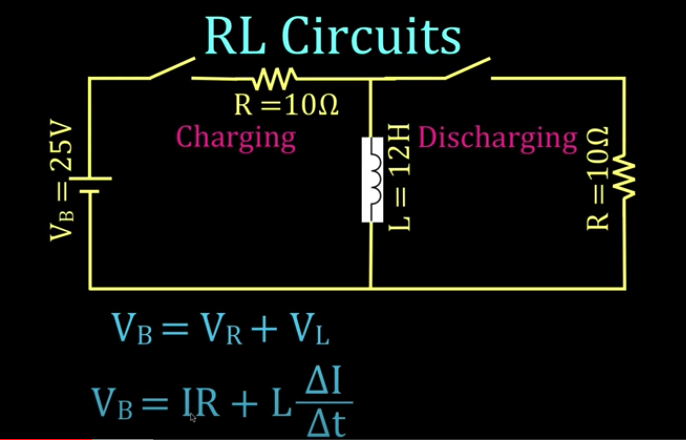
Charging an Inductor

$\tau =\frac{L}{R}$

$V_t=V_s(e^{\frac{-tR}{L}})$