Singular Value Decomposition Youtube Playlist

1. Singular Value Decomposition Overview

Helps with data reduction, dimensionality reduction, and as a foundation and as a foundation of ML
Most used general purpose tool in Linear Algebra for processing
Think of it it as a data reduction tool
SVD will help reduce this data into the key features for analyzing and describing this data
One of the first steps in dimensionality reduction and ML techniques
the SVD is a data driven generalization of the Fast Fourier Transform
Think of them as tailored to the specific problem
Lot of features in common with the FFT, but more specific to the data we have access to
One thing you can do is use it to solve matrix equations for non-square A matrices
This works well for linear regression models
Can also use it as basis for PCA (principle component analysis)
We will talk a lot about correlation
It's used everywhere. FB, GOOGLE, Microsoft
One of the most important things if you want to use Linear Algebra to make money
Simple and interpretable Linear Algebra

2. Singular Value Decomposition: Mathematical Overview

video

$X$ is defined as a collection of column vectors

Example

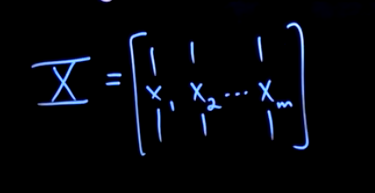
Say you have a 1 megapixel image of someone's face. You could shape that into a single column, million pixel row column vector. This would be $x_{1}$ you could repeat for $m$ people up to $x_{m}$
$x_{k} \in R^{n}$ N will be the dimension of your data set (ie 1 million) by m columns

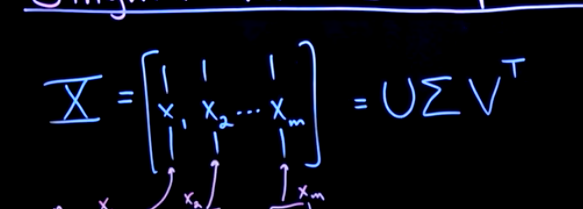
The SVD will let us take the matrix $X$ and represent it as the product of 3 other matrices ( $U Σ V^{T}$ )

The $U$ matrix and the $V$ matrix are what are called "unitary" matrices, or orthogonal matrices, and $Σ$ is a diagonal matrix

Since there are only $M$ columns of $X$ there will be only $m$ non-zero values in $Σ$
The columns of $U$ have the same shape as a column of $X$ ...so if $X_{1}$ is a million x 1 vectors, $U$ will be a million x 1 vectors. These would be "eigen values"

Unitary means $U U^{T} = U^{T} U = I I$ the columns provide a complete basis for all of N. $U$ is an $n \times m$
This also holds for $V$ ... $V V^{T} = V^{T} V = I I$ $V$ is a $m \times m$
$Σ$ is diagonal and is non-negative in hierarchical value. $σ_{1} \geq σ_{2}$

Which means the first columns of $U$ , $V$ , and $Σ$ are more important then the next columns
$U$ is left singular vectors
$V$ is right singular vectors
$Σ$ is a matrix of singular values

If some of the sigma values are very small we can essentially ignore them because they are ordered by importance

In talking about flows
$V$ would be like a snapshot in time of the values of $X$
In talking about faces, the first column of $V^{T}$ would be a mixture of all the columns of $U_{1}$ you would have to add up to equal $X_{1}$

Easy to compute in matlab and python

[USV] = svd(X);

They are guaranteed to exist and unique