Tree Traversal

There are 3 main traversal types for trees

Pre-Order Traversal

The tree will first read the root, then the left child, then the right child.

Pre-Order Snippet

traverse(TreeNode *root){
if(root == NULL) return;
traverse(root->left);
traverse(root->right);
}

In-Order Traversal

The tree will read the left child, then the root, then the right child.

In-Order Snippet

traverse(TreeNode *root){
traverse(root->left);
if(root == NULL) return;
traverse(root->right);
}

Post-Order Traversal

The tree will read the left child, then the right, then the root.

Post-Order Snippet

{
traverse(root->left);
traverse(root->right);
traverse(TreeNode *root)
if(root == NULL) return;
}

Level Ordered Traverse

In a level ordered traverse, you're visiting level by level. To do this, we need to employ a FIFO Data Structure. In this case, we will be using a Queue.

Level ordered traversals are Breadth First Search

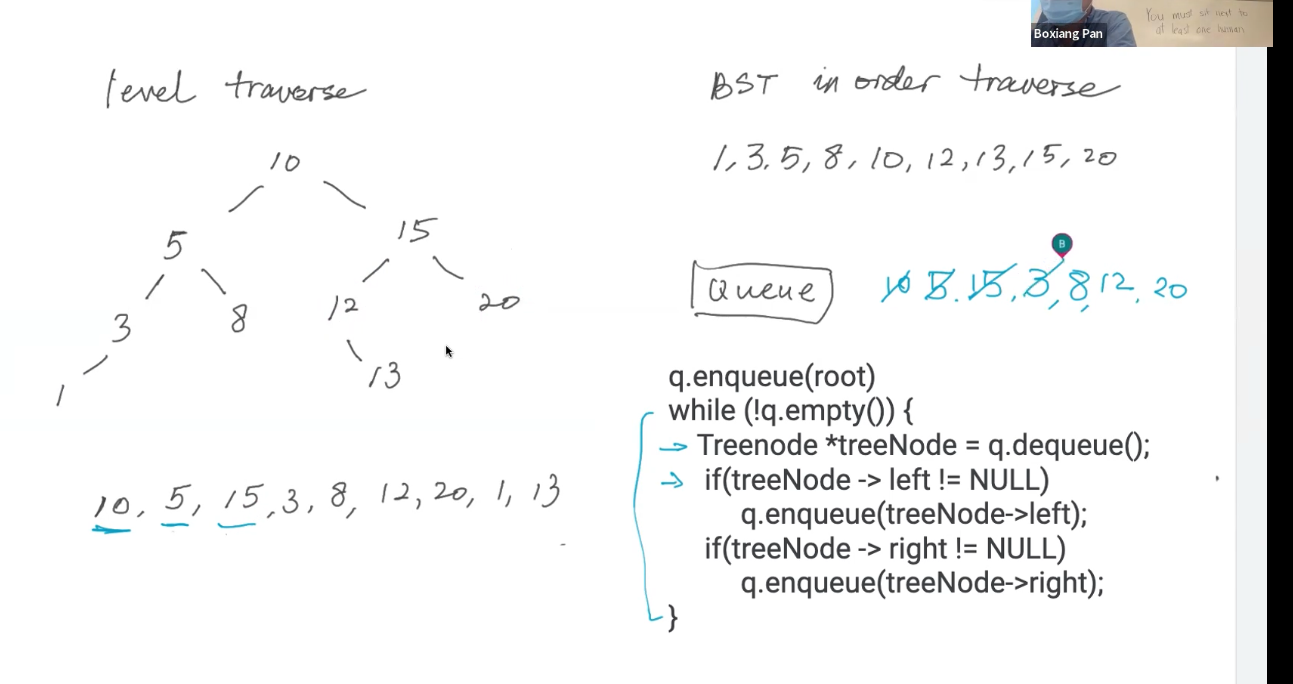
Level Traverse Snippet

q.enqueu(root)
while(!q.empty()){
Treenode *treeNode = q.dequeue();
if(treeNode ->left !=NULL){
	q.enqueue(treeNode->left);
	};
if(treeNode -> right!=NULL){
	q.enqueue(treeNode->right);
	};

}

With the above code however, we don't know how deep the tree goes. We need a tracker for the queue size

q.enqueu(root)
int level = 0
while(!q.empty()){
int sz = q.size();
	for(i=1,i<sz,i++){
		Treenode *treeNode = q.dequeue();
			if(treeNode ->left !=NULL){
				q.enqueue(treeNode->left);
			};
			if(treeNode -> right!=NULL){
			q.enqueue(treeNode->right);
			};
	}

level++
}

LeetCode Problem 26 - Remove Duplicates from Sorted Array Problems

104 Maximum Depth of a Binary Tree

https://leetcode.com/problems/maximum-depth-of-binary-tree/

When we see a tree problem, usually there are 2 approaches:

1. Traverse the Tree

int res = 0;
int depth = 0; //This is the depth of the current TreeNode

void traverse(TreeNode* root)
{
	if(root == NULL){
		//at leaf node, update the result
		res=max(res,depth);
		return;
	}
depth++;
traverse(root->left);
traverse(root->right);
}

int maxDepth(TreeNode* root){
traverse(root);
return res
}

2. Divide into sub problems(recursion)

int maxDepth(TreeNode *root){
	if(root == Null){
	//base case
	return 0;
	}
	int leftDepth = maxDepth(root->left);
	int rightDepth = maxDepth(root->right);
	return max(leftDepth, rightDepth) + 1;
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        
    }
};

Since the return value is usually the answer to the problem, we use Post Order

543 Diameter of a Binary Tree

https://leetcode.com/problems/diameter-of-binary-tree/

Approach 1: Traverse (O($n^2$))

int maxDiameter = 0;
int diameterOfBinaryTree(TreeNode *root){ 
	traverse(root);
	return maxDiameter
}

void traverse(TreeNode *root){
if(root == NULL){
	return;
}
int leftDepth = maxDepth(root->left);
int rightDepth = maxDepth(root->right);
maxDiameter = max(maxDiameter, leftDepth+rightDepth);

traverse(root->left);
traverse(root->right);
}

int maxDepth(TreeNode* root){
if(root == NULL){
	return 0;
}
int leftDepth = maxDepth(root->left);
int rightDepth = maxDepth(root->right);
return max(leftDepth,rightDepth) + 1;
}

Approach 2: Sub Problems (O(n))

int maxDiameter = 0;
int diameterOfBinaryTree(TreeNode* root){
	maxDepth(root);
	return maxDiameter;
}

int maxDepth(TreeNode* root){
	if(root == NULL){
		return 0;
		}
		int leftDepth = maxDepth(root->left);
		int rightDepth = maxDepth(root->right);
		maxDiameter = max(maxDiameter, leftDepth+rightDepth);
		return 1 + max(leftDepth,rightDepth);
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int diameterOfBinaryTree(TreeNode* root) {
        
    }
};

226 Invert Binary Tree

Approach 1: Traversal

TreeNode* invertTree(TreeNode* root){
traverse(root);
return root;
}


void traverse(TreeNode* root){
if(root == NULL){
	return;
}
TreeNode* tmp = root->left
root->left = root->right
root->right = tmp;

traverse(root->left);
traverse(root->right);
}

Approach 2: SubProblems

TreeNode* invertTree(TreeNode* root){
	if(root==NULL){
	return NULL;
	}
	TreeNode* left = invertTree(root->left);
	TreeNode* right = invertTree(root->right);
	root->left = right;
	root->right = left;
	return root;
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        
    }
};